文章详情页 您现在的位置是:网站首页>文章详情
LMS自适应对消算法
![]() 邓鑫
发表于:2019年10月28日 10:22
分类:【算法】
7579次阅读
邓鑫
发表于:2019年10月28日 10:22
分类:【算法】
7579次阅读
LMS算法最小均方误差算法,是一种自适应滤波算法。该算法通过对输入信号进行滤波输出一个信号y(n),将输出信号与期望输出信号作差得到一个误差信号,再将误差信号输入到自适应滤波器中形成一个反馈回路。LMS算法就通过取得最小均方误差得到的一种算法。算法过程:
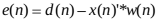 (1)
(1)
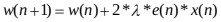 (2)
(2)
其中,式中e(n)、d(n)、x(n)、w(n)分别代表期望信号与滤波器输出信号的误差、期望信号、输入信号和滤波器权值因子。式(2)表示抽头权向量的更新公式,其中λ为迭代步长,取值范围为 0 < λ < 1/λmax。λmax表示输入信号的能量。通常情况下 λ 的是跟据经验来确定的,是一个在0到1之间的数。LMS算法步长调整原则:滤波器的收敛速度和稳态误差是一对矛盾。当拥有较大的步长因子会加快滤波器的收敛速度,但同时也会增大稳态失调误差。较小的步长因子会减小滤波器的收敛速度但会拥有较小的稳态误差。
为了克服这一矛盾,在现有固定步长算法的基础上我们提出了新的算法—变步长自适应算法。其优点是步长值随误差的改变而改变。在误差较大的时候步长因子也大以获得更快的收敛速度;当收敛过程接近稳态,误差小的时候其步长因子也小以获得较小的稳态误差。
在固定步长的LMS算法中引入基于正弦函数的步长更新公式:
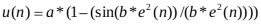 (3)
(3)
其中参数a用来控制步长大小,参数b用来调整参数变化率的[2]。u(n)的变化也应该服从固定步长时 λ 的取值要求:0 < λ < 1。该方法在迭代初始时拥有较大速度,在稳态时有较小的稳态误差。
2自适应噪声对消原理
对消器原理如图1所示,对消器由两个传感器组成,其中一个传感器用来接收信号发送端经信道传送过来的信号s和引入的不相关的噪声信号 n0,组成原始输入信号s + n0 。另一个信号是用来接收与n0相关的噪声信号n1,n1是用来给对消器提供一个参考输入。在自适应滤波过程中,滤波器对n1进行滤波产生一个与n0相近似的信号输出y。将输出信号y与输入信号s + n0相减得到误差信号 e(n)。
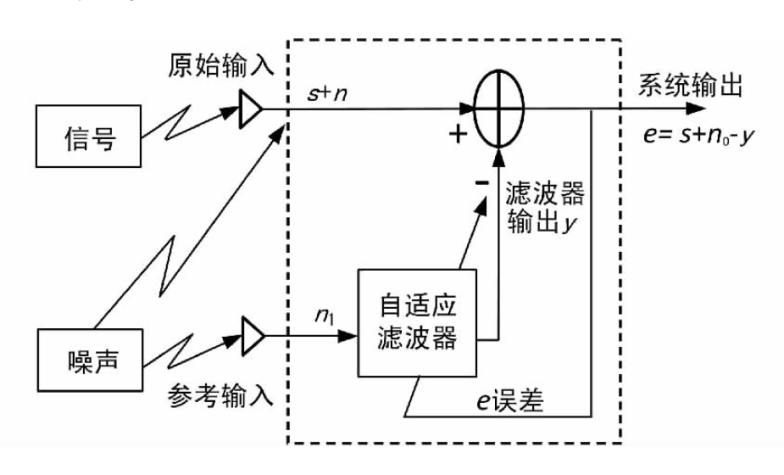
图1 自适应对消原理
3算法仿真
自适应FIR滤波器阶数为2,输入信号s(n)=sin(2πn),输入噪声信号n0(n)为均值为0,方差为0.5的高斯噪声。分别用两种LMS算法对噪声进行消除。
固定步长LMS算法迭代方程:
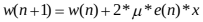 (8)
(8)
经过大量仿真比较得出 μ=0.02 时收敛特性较好。
变步长LMS算法迭代方程:
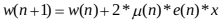 (9)
(9)
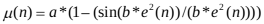 (10)
(10)
通过MATLAB仿真得到参数a、b的最佳参数分别为0.1和1.1。
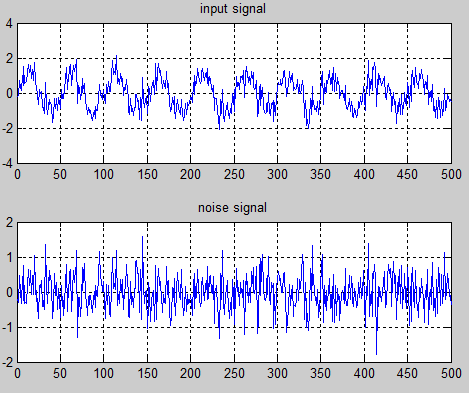
图2 输入噪声信号和叠加噪声的输入信号

图3 期望信号
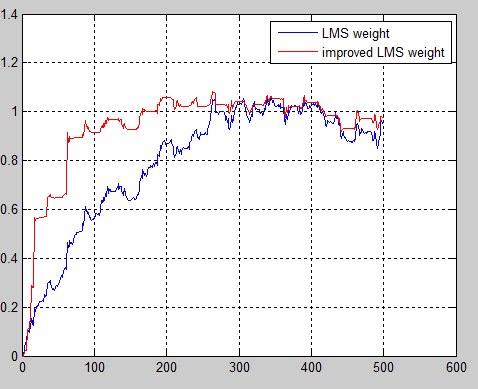
图4 权值收敛过程
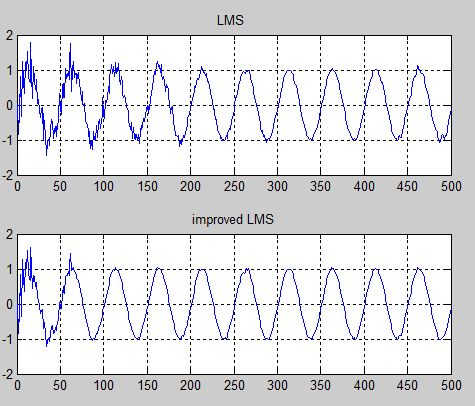
图5 两种算法滤波后的效果
由图5两种算法滤波去噪后的效果也可以看出改进的变步长LMS算法的收敛速度更快,同时从图4中可以看出在两种算法都收敛稳定的时候,受到外界噪声干扰的时候改进的LMS算法具有更强的抗外界噪声干扰的特性和更小的稳态误差。
详细程序如下:
% %generate a input signal
% %generate two relative wgn as noise signal
clc
clear
close all
k=0:0.02:10-0.02;
N=length(k);
user=sin(2*pi*k);
n0=normrnd(0,0.3,1,N);
receive=n0+user; %receive useful signal and noise
M=2; %filter order
%LMS
lmd=0.02;
e1=zeros(1,N);
w1=zeros(N,M);
se1=zeros(1,N);
for n= M: N
x=n0(n:-1:n-M+1);
y(n)=x*w1(n,:)';
e1(n)=receive(n)-y(n);
w1(n+1,:)=w1(n,:)+2*lmd*e1(n)*x;
end
% improved LMS
e2=zeros(1,N);
w2=zeros(N,M);
for n= M: N
x=n0(n:-1:n-M+1);
y(n)=x*w2(n,:)';
e2(n)=receive(n)-y(n);
u(n)=0.1*(1-(sin(1.1*e2(n)^2))/(1.1*e2(n)^2));
w2(n+1,:)=w2(n,:)+2*u(n)*e2(n)*x;
end
figure
plot(user)
grid on
figure
subplot(2,1,1)
plot(receive);grid on;
title('input signal');
subplot(2,1,2)
plot(n0);grid on;
title('noise signal');
figure
subplot(2,1,1)
plot(e1);grid on;
title('LMS ');
subplot(2,1,2)
plot(e2);grid on;
title('improved LMS');
figure
plot(w1(:,1));
hold on
plot(w2(:,1),'r');
grid on;
legend('LMS weight','improved LMS weight ')版权声明 本文属于本站 原创作品,文章版权归本站及作者所有,请尊重作者的创作成果,转载、引用自觉附上本文永久地址: http://blog.lujianxin.com/x/art/fi6otdx04sev
上一篇:我在杭州叙事火影忍者篇
下一篇:我在杭州叙事老楼梯篇
猜你喜欢
文章评论区
作者名片
- 作者昵称:邓鑫
- 原创文章:1篇
- 转载文章:0篇
- 加入本站:2442天
作者其他文章
站长推荐
友情链接
站点信息
- 运行天数:2446天
- 累计访问:164169人次
- 今日访问:0人次
- 原创文章:69篇
- 转载文章:4篇
- 微信公众号:第一时间获取更新信息

